ナイル川の氾濫は「ピタゴラスの定理」と繋がっています。
「なにこれ?」と思う人が多いでしょうね。
ピタゴラスの定理の原点はエジプト・ナイル川の測量術と繋がるのです。
日常生活に中で生まれた知恵が、昇華され「学問」になったのです。
「共通テスト」で求められている思考力や判断力とは、こうした力です。
今回は「日常生活に繋がった学び」について考えてみよう。
日常生活の中で生まれた知恵
久しぶりに、エジプトで仕事をしている教え子から便りがきました。
この国の治安はまだ安定せず、日々の暮らしも落ち着かないそうです。
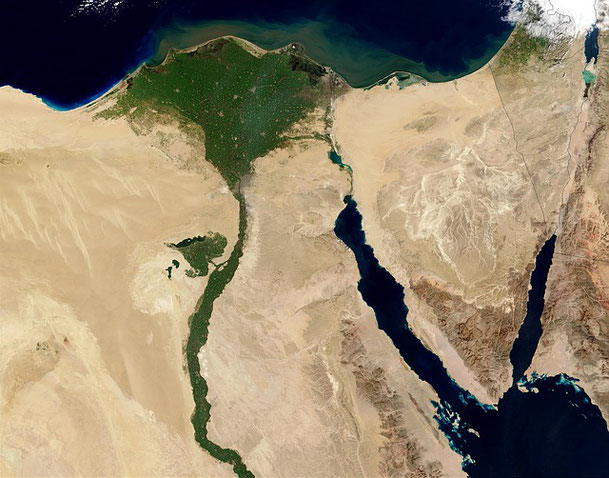
首都カイロから.1時間くらいのところに、ギザのピラミッドがあります。
壮大な風景は旧いナイル川のほとりです。
この巨大な建築物を、4000年以上も前の人々がどのようにして造ったのでしょうか。
高度の測量機器がない時代だから「日常生活の中で生まれた知恵」を集めて改良・改善を進め壮大で巨大なピラミッドをつくったと考えられるわけです。
ナイル川の氾濫は、日本の河川のように「一度にドーッ」とくるものではないのです。
7月の下旬から数か月かけて「徐々に水が増えて」、河床があがっていくのです。
上流の山々の雪解けに合わせて、川が氾濫していく。
やがて、小高い丘を残して水没します。川幅は、7~8倍になったそうです。
数カ月後、今度は、徐々に水がひいていきますから、灌漑用の溜池をつくったり、小麦の種まきを一斉にしたりします。
大規模な農作業を短期間に一挙にしなくてはなりません。
また、河川の氾濫の間に、区画が滅茶苦茶になってしまうので、測量を行い、区画を作り直す必要がありました。
生活上の必要性から、測量技術が生まれました。
分かり易く言えば、シリウス星を基点として、「直角三角形」を用いて地面を測量したのです。
こうして、水準測定器・垂直確定器・定規といった、測量に必要な機器が生まれたのでビラミッド建設ができたのですね。
ピラミッドは完全な水平が保たれ、東西南北の誤差は1cm以内に収まっているそうです。凄いですね。
みなさんも糸で「直線を12」に区切って直角三角形をつくってください。
<3:4:5>の形ができましたか?
これが、「ピタゴラスの定理」の原型で幾何学の出発点になったと考えると楽しいですね。
勿論、細かな学説は省いていますから、関心がある人は自分で調べてくださいね。
原点を追及せよ
ナイルメーターを知っていますか?
川の水が、どの辺まで来たら氾濫が止まるのか。
いつから、種まきをしなければならないか。
「経験知をデータ」にしたものです。
天空の星座の動きを観察し、自然の動きをチェックして生活の知恵とする。
私たちが「科学」とよんでいるものは、こうした観測や実験を積み重ねてできたものです。
日常生活の中に転がっている課題・テーマにもう一度目を光らせると、ものすごくたくさんの知恵が転がっているのですね。
こうした能力を再認識させようと「共通テスト」はテーマの1つにしています。
ピタゴラスはギリシャの哲学者であり宗教家です。
彼は宇宙を幾何学で説明しようとした学者です。
エジプトの測量術を学問として昇華したと考えてよいと思います。
勿論、数学は実利ばかリが優先する学問ではありません。
私は「なぜタレスは、『万物の根源は水である』といったのかと疑問に思い、現在のトルコのミレトスに行った」ことがあります。
古代ギリシャで発達した高度の学問への関心は、大学入試が終わったら勉強してください。
こうした「原点の追求」こそ、これからの時代に期待されることですからね。
私は、世界各地に行って、肌でいろいろなことを受けとめてくることを勧めます。
世界は広く、興味深いことばかりです。観光だけでもいい。
もう一歩掘り下げて「現地で考える」方がもっといいです。
エジプトは、ナイル川にアスワンダム・ハイダムができてから、気象が一挙に変わってしまいました。
ナイル川の氾濫はなくなりましたが、需要な幹線道路だった役割もなくなり、寄生虫がウヨウヨいる川に代わりました。川幅は狭くなり、砂漠化が止まりません。
それがよかったのか、悪かったのか。
現地で考えてみてください。
それが次代を担うみなさんの重要な仕事です。


コメントをお書きください